23년 5급 인공지능 해설

혼돈 행렬에 관한 문제다. 혼돈 행렬이 나오면 무조건 다음 표는 암기해야 하고, 이 표만 암기하면 웬만해선 문제를 틀릴 일이 없다.
| 실제값 | |||
| True | False | ||
| 예측값 | True | True Positive | False Positive |
| False | False Negative | True Negative | |
- 특이도 : TN / ( TN + FP )
- 민감도(재현율) : TP / ( TP + FN )
- 정밀도(TPR) : TP / ( TP + FP )
1)
F1 score의 수식은 2×(민감도 ×정밀도)/(민감도+정밀도)이다. 그런데 문제에서 주어진 데이터로 계산할 수 없는 이유를 설명하라고 했다. 그래서 답에 대한 플롯은 F1 score를 구성하는 수식 중 일부가 문제에서 제시하지 않았기 때문이라고 짐작할 수 있다. 자세한 설명은 그 플롯에 살을 붙여 나가는 식으로 작성하면 된다.
F1 score를 구하기 위해서는 민감도와 정밀도를 구해야 한다. 그런데 문제에서 주어진 데이터는 민감도와 위양성률이다. 위양성률(FPR)은 FP / ( FP + TN )으로, 모델 A를 예시로 들어 왜 F1 score를 구할 수 없는지 설명해본다. 재현율 = TP / ( TP + FN ) = 0.3을 통해 TP와 FN의 비를 알 수 있다. 또한, 위양성률 = FP / ( FP + TN ) = 0.6을 통해 FP와 TN의 비를 알 수 있다. TP : FN = 3 : 7 이며 FP : TN = 6 : 4이다. 따라서 TP = 3x, FN = 7x, FP = 6y, TN = 4y라고 쓸 수 있는데 x, y의 값을 정확하게 알 수는 없다. 따라서 F1 score의 값을 정확히 알 수 없다.
2)
특이도 = (1 - 위양성률)이므로 A = 0.4, B = 0.2, C = 0.8, D = 0.2

전형적인 신경망에 관한 문제다. 활성화 함수는 ReLU 함수와 항등 함수를 사용하였다. 문제에서 설명하는 신경망의 구조를 다음과 같이 그려보면 문제 푸는 것은 쉽다.
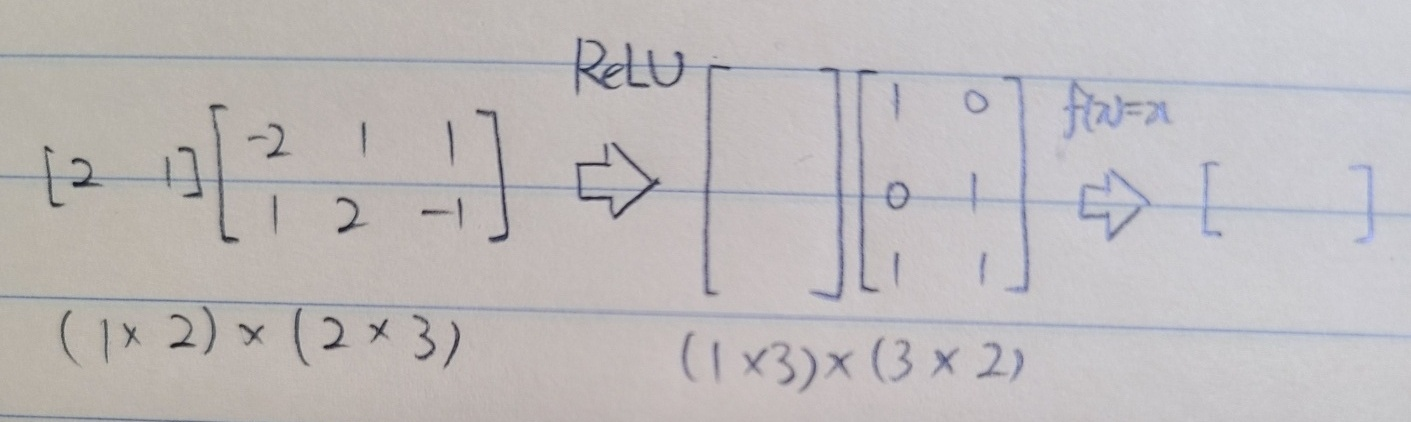
1)
ReLU 함수와 sigmoid 함수의 식은 다음과 같다.


두 함수를 활성화 함수로서 비교를 해보면, sigmoid 함수는 -1과 1 사이의 값을 치역으로 갖는 함수로 S자형 곡선을 나타낸다. 사실 sigmoid 함수도 출력값이 일정하며, y=1 과 y=-1에 대해 상, 하한으로 수렴하기 때문에 활성화 함수로 쓰이기에 그렇게 나쁘지 않은 함수다.
다만 요즘 sigmoid 함수를 활성화 함수로 거의 쓰이지 않는 이유는 딥러닝이 발달하면서 신경망이 깊어지고 복잡해진 것에 그 연유를 찾을 수 있다. 신경망이 복잡해질수록 역전파 과정에서 미분 연산이 중첩되는데, 그 과정에서 vanishing gradient 문제가 발생할 수 있기 때문이다.
Vanishing Gradient 문제는 은닉층이 더해질수록 미분 연산이 반복되어 결국 weight가 제대로 갱신되지 않는 현상을 의미한다. Sigmoid 함수의 도함수는 최댓값이 x=0 일때 0.3인데, 이 연산이 계속 반복되다 보면 0.3, 0.09, 0.0027, ... (가장 느리게 줄어드는 것이 이 정도) 이런 식으로 다음 층에서 가중치가 갱신되는 정도가 점점 줄어들 것이다.
반면 ReLU 함수의 도함수는 0, 1 2개의 값만 가지므로 상대적으로 vanishing gradient 문제에서 자유롭다는 장점이 있다. 그래서 요즘 딥러닝의 활성화 함수는 대부분 ReLU 계열의 함수를 쓴다. 물론 ReLU 함수도 만능은 아닌 것이, 데이터에 음수가 많다면 도함수도 0이 많아지므로 학습이 제대로 안될 수 있는데, 그 때는 LeakyReLU와 같은 다른 종류의 활성화 함수를 사용하면 된다.
2) 그래서 신경망의 출력값은 얼마? [1 5]

K-means 알고리즘을 맨해튼 거리를 이용해 군집화에 적용하는 문제다. 문제는 k-means 알고리즘의 동작 단계를 기술하고, 그것을 실제로 적용하는 식으로 구성되어 있다. 아, 참고로 7급에서도 똑같은 내용을 묻는 문제가 출제되었다.
1) K-means 알고리즘의 동작 단계
- 1. k개의 임의의 중심점을 설정한 다음, 각 데이터 포인트~중심점 까지의 거리를 계산한다.
- 2. 가장 가까운 중심점에 그 데이터 포인트를 소속시킨다.
- 3. 각 중심점에 소속된 데이터 포인트들의 평균을 계산하여 새로운 중심점을 계산한다.
- 1~3번의 과정을 소속 데이터 포인트가 변하지 않을 때까지 반복한다.
2) A(3, 9), B(4, 6), C(5, 15), D(6, 10), E(7, 7), F(8, 15), G(9, 16), H(9, 11)
문제에서는 초기 중심점 좌표를 줬다. C와 E를 제외한 나머지 점들과의 맨해튼 거리를 계산하여 가장 가까운 중심점을 찾아보자.
C : C(5, 15), F(8, 15), G(9, 16)
E : A(3, 9), B(4, 6), D(6, 10), E(7, 7), H(9, 11)
각 데이터 포인트의 평균을 계산하면 다음과 같다.
C' : (7, 15) → C, F, G, H
E' : (5, 8) → A, B, D, E
새로운 포인트가 갱신되었다. 이 갱신된 포인트를 바탕으로 중심점을 다시 계산하면
C'' : (7, 14) → C, F, G, H
E'' : (5, 8) → A, B, D, E
여기서부터는 중심점에 속하는 데이터 포인트 집합이 변하지 않는다. 따라서 K-means 알고리즘은 여기서 멈춘다.